import pandas as pd
import numpy as np
import warnings
import matplotlib.pyplot as plt
warnings.filterwarnings('ignore')
%matplotlib inline

Decision Tree and Ensemble Learning

Decision Tree

A decision tree may be described as a set of decisions/categorization steps that help you to classify your data into predefined classes. This helps you to solve a classification problem.

For example, consider the following data set related to playing tennis in a specific day based on weather condition parameters. Based on the provided parameters, we are need to come up with a decision tree that helps us to decide whether the player plays tennis on a specific day based on four weather related parameters including outlook, temperature, humidity and wind condition.

data_dict = {
    'Outlook' : ['Sunny', 'Sunny', 'Overcast', 'Rainy', 'Rainy', 'Rainy', 'Overcast', 'Sunny', 'Sunny','Rainy', 'Sunny', 'Overcast', 'Overcast', 'Rainy']
    ,'Temperature': ['Hot', 'Hot', 'Hot', 'Mild', 'Cool', 'Cool', 'Cool', 'Mild', 'Cool', 'Mild','Mild','Mild', 'Hot', 'Mild']
    ,'Humidity' : ['High', 'High', 'High', 'High', 'Normal', 'Normal', 'Normal', 'High','Normal','Normal', 'Normal', 'High', 'Normal', 'High']
    ,'Wind': ['False', 'True', 'False', 'False', 'False', 'True', 'True', 'False', 'False', 'False', 'True', 'True', 'False', 'True']
    ,'PlayTennis': ['No', 'No', 'Yes', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes', 'Yes', 'Yes', 'Yes', 'Yes', 'No']
}
tennis_data = pd.DataFrame(data_dict, columns=data_dict.keys())
tennis_data

	Outlook	Temperature	Humidity	Wind	PlayTennis
0	Sunny	Hot	High	False	No
1	Sunny	Hot	High	True	No
2	Overcast	Hot	High	False	Yes
3	Rainy	Mild	High	False	Yes
4	Rainy	Cool	Normal	False	Yes
5	Rainy	Cool	Normal	True	No
6	Overcast	Cool	Normal	True	Yes
7	Sunny	Mild	High	False	No
8	Sunny	Cool	Normal	False	Yes
9	Rainy	Mild	Normal	False	Yes
10	Sunny	Mild	Normal	True	Yes
11	Overcast	Mild	High	True	Yes
12	Overcast	Hot	Normal	False	Yes
13	Rainy	Mild	High	True	No

The following decision three helps us to use a set of decisions to solve our classification problem.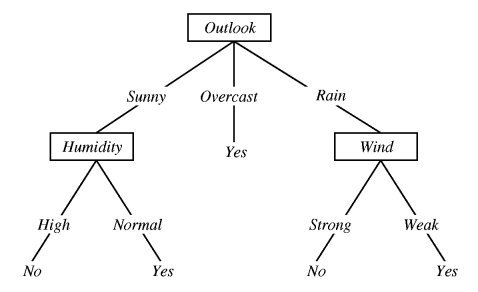

Order of decision; why Outlook is the first question/decision?

The main question is why outlook was chosen as the first decision level. The answer is that the amount of Information Grain that is resolved by this decision is higher that the other decisions. This can be quantified using entropy which is a measure of randomness. Higher entropy means higher randomness and the amount of reduction in randomness based on a decision is called information gain.

%%latex

Entropy = $-\sum_{i=1}^{n} P_i\times Log_b(P_i)$

Entropy = $-\sum_{i=1}^{n} P_i\times Log_b(P_i)$

Note: corresponding units of entropy are the bits for b = 2, nats for b = e, and bans for b = 10 where b is the base of the logarithm function

def entropy_calculate(prob_list):

    entropy = 0
    for item in prob_list:
        entropy -= item * np.log2(item)
    return entropy

Entropy of the entire system

Entropy of the entire system: 14 observations: 9 Yes and 5 No

cases,counts = np.unique(tennis_data.PlayTennis,return_counts=True)
P = [count/len(tennis_data) for count in counts]
print('Probabilities of %s and %s are %.3f, %.3f respectively'%(cases[0],cases[1],P[0],P[1]))

entropy_entire = entropy_calculate(P)

print('Entire syetems entropy is %.3f bits'%entropy_entire)

Probabilities of No and Yes are 0.357, 0.643 respectively
Entire syetems entropy is 0.940 bits

Information Gain

Lets calculate reduction in entropy for each decision. For each decision, entropy is calculated for each case under that decision and the a probability weighted average is calculated.

Outlook decision

cases_outlook,counts_outlook= np.unique(tennis_data.Outlook,return_counts=True)
P_outlook = [count/len(tennis_data) for count in counts_outlook]
print('For outlook:')
for case, prob in zip(cases_outlook,P_outlook):
    print('\tProbabality of %s is %.3f'%(case, prob))

For outlook:
        Probabality of Overcast is 0.286
        Probabality of Rainy is 0.357
        Probabality of Sunny is 0.357

entropy_outlook={}
total_entropy_outlook=0
for case, prob in zip(cases_outlook,P_outlook):
    cases,counts = np.unique(tennis_data.PlayTennis[tennis_data.Outlook==case],return_counts=True)
    P = [count/len(tennis_data[tennis_data.Outlook==case]) for count in counts]
    entropy_outlook[case]=entropy_calculate(P)
    total_entropy_outlook += entropy_calculate(P)*prob

for case, entropy in entropy_outlook.items():
    print('Entropy for %s is %.2f'%(case,entropy))
print('\nEntropy at Outlook decision level is %.3f'%total_entropy_outlook)
print('\nInformation gain is %.3f'%(entropy_entire- total_entropy_outlook))

Entropy for Overcast is 0.00
Entropy for Rainy is 0.97
Entropy for Sunny is 0.97

Entropy at Outlook decision level is 0.694

Information gain is 0.247

Temperature Decision

cases_temperature,counts_temperature= np.unique(tennis_data.Temperature,return_counts=True)
P_temperature = [count/len(tennis_data) for count in counts_temperature]
print('For temperature:')
for case, prob in zip(cases_temperature,P_temperature):
    print('\tProbabality of %s is %.3f'%(case, prob))

For temperature:
        Probabality of Cool is 0.286
        Probabality of Hot is 0.286
        Probabality of Mild is 0.429

entropy_temperature={}
total_entropy_temperature=0
for case, prob in zip(cases_temperature,P_temperature):
    cases,counts = np.unique(tennis_data.PlayTennis[tennis_data.Temperature==case],return_counts=True)
    P = [count/len(tennis_data[tennis_data.Temperature==case]) for count in counts]
    entropy_temperature[case]=entropy_calculate(P)
    total_entropy_temperature += entropy_calculate(P)*prob

for case, entropy in entropy_temperature.items():
    print('Entropy for %s is %.2f'%(case,entropy))
print('\nEntropy at Temperature decision level is %.3f'%total_entropy_temperature)
print('\nInformation gain is %.3f'%(entropy_entire- total_entropy_temperature))

Entropy for Cool is 0.81
Entropy for Hot is 1.00
Entropy for Mild is 0.92

Entropy at Temperature decision level is 0.911

Information gain is 0.029

Wind Decision

cases_wind,counts_wind= np.unique(tennis_data.Wind,return_counts=True)
P_wind = [count/len(tennis_data) for count in counts_wind]
print('For wind:')
for case, prob in zip(cases_wind,P_wind):
    print('\tProbabality of %s is %.3f'%(case, prob))

For wind:
        Probabality of False is 0.571
        Probabality of True is 0.429

entropy_wind={}
total_entropy_wind=0
for case, prob in zip(cases_wind,P_wind):
    cases,counts = np.unique(tennis_data.PlayTennis[tennis_data.Wind==case],return_counts=True)
    P = [count/len(tennis_data[tennis_data.Wind==case]) for count in counts]
    entropy_wind[case]=entropy_calculate(P)
    total_entropy_wind += entropy_calculate(P)*prob

for case, entropy in entropy_wind.items():
    print('Entropy for %s is %.2f'%(case,entropy))
print('\nEntropy at Wind decision level is %.3f'%total_entropy_wind)
print('\nInformation gain is %.3f'%(entropy_entire- total_entropy_wind))

Entropy for False is 0.81
Entropy for True is 1.00

Entropy at Wind decision level is 0.892

Information gain is 0.048

Humidity Decision

cases_humidity,counts_humidity= np.unique(tennis_data.Humidity,return_counts=True)
P_humidity = [count/len(tennis_data) for count in counts_humidity]
print('For humidity:')
for case, prob in zip(cases_humidity,P_humidity):
    print('\tProbabality of %s is %.3f'%(case, prob))

For humidity:
        Probabality of High is 0.500
        Probabality of Normal is 0.500

entropy_humidity={}
total_entropy_humidity=0
for case, prob in zip(cases_humidity,P_humidity):
    cases,counts = np.unique(tennis_data.PlayTennis[tennis_data.Humidity==case],return_counts=True)
    P = [count/len(tennis_data[tennis_data.Humidity==case]) for count in counts]
    entropy_humidity[case]=entropy_calculate(P)
    total_entropy_humidity += entropy_calculate(P)*prob

for case, entropy in entropy_humidity.items():
    print('Entropy for %s is %.2f'%(case,entropy))
print('\nEntropy at Humidity decision level is %.3f'%total_entropy_humidity)
print('\nInformation gain is %.3f'%(entropy_entire- total_entropy_humidity))

Entropy for High is 0.99
Entropy for Normal is 0.59

Entropy at Humidity decision level is 0.788

Information gain is 0.152

As shown above, by choosing outlook as the first decision/question, the highest reduction in entropy/randomness is achieved that corresponds to the highest Information Gain

Titanic Example

import urllib3
import pandas as pd
import certifi
import re
from bs4 import BeautifulSoup
import warnings
warnings.filterwarnings('ignore')

Loading data using BeautifulSoup and urlib3 as the htm client

html_address = 'https://www.encyclopedia-titanica.org/titanic-passengers-and-crew/'

http = urllib3.PoolManager(maxsize=10, cert_reqs='CERT_REQUIRED',ca_certs=certifi.where())
r = http.request('GET', html_address)

soup = BeautifulSoup(r.data, 'html.parser')

table = soup.find('table')
data = pd.read_html(str(table),flavor='bs4')[0] # Note that the flavor cotains information about the encoding as well
http.clear()
data.head()

	Name	Age	Class/Dept	Ticket	Joined	Job	Boat [Body]	Unnamed: 7
0	ABBING, Mr Anthony	42	3rd Class Passenger	5547£7 11s	Southampton	Blacksmith	NaN	NaN
1	ABBOTT, Mrs Rhoda Mary 'Rosa'	39	3rd Class Passenger	CA2673£20 5s	Southampton	NaN	A	NaN
2	ABBOTT, Mr Rossmore Edward	16	3rd Class Passenger	CA2673£20 5s	Southampton	Jeweller	[190]	NaN
3	ABBOTT, Mr Eugene Joseph	13	3rd Class Passenger	CA2673£20 5s	Southampton	Scholar	NaN	NaN
4	ABBOTT, Mr Ernest Owen	21	Victualling Crew	NaN	Southampton	Lounge Pantry Steward	NaN	NaN

data_trim = data[['Name', 'Age', 'Class/Dept', 'Boat [Body]']]
data_trim.head()

	Name	Age	Class/Dept	Boat [Body]
0	ABBING, Mr Anthony	42	3rd Class Passenger	NaN
1	ABBOTT, Mrs Rhoda Mary 'Rosa'	39	3rd Class Passenger	A
2	ABBOTT, Mr Rossmore Edward	16	3rd Class Passenger	[190]
3	ABBOTT, Mr Eugene Joseph	13	3rd Class Passenger	NaN
4	ABBOTT, Mr Ernest Owen	21	Victualling Crew	NaN

Processing data

Special characters are removed and then the age is change to float and ages below 1 year are converted to a representative float number

data_trim['Name'] = data_trim['Name'].map(str).apply(lambda x: x.encode('utf-8').decode('ascii', 'ignore'))
data_trim['Boat [Body]'] = data_trim['Boat [Body]'].map(str).apply(lambda x: x.encode('utf-8').decode('ascii', 'ignore'))
def process_age(value):
    if 'm' in value:
        return float(re.findall(r'-?\d+\.?\d*',value)[0])/12
    else:
        return(float(value))
data_trim['Age'] = data_trim['Age'].map(str).apply(process_age)

data_trim.head()

	Name	Age	Class/Dept	Boat [Body]
0	ABBING, Mr Anthony	42.0	3rd Class Passenger	nan
1	ABBOTT, Mrs Rhoda Mary 'Rosa'	39.0	3rd Class Passenger	A
2	ABBOTT, Mr Rossmore Edward	16.0	3rd Class Passenger	[190]
3	ABBOTT, Mr Eugene Joseph	13.0	3rd Class Passenger	nan
4	ABBOTT, Mr Ernest Owen	21.0	Victualling Crew	nan

Categorize passengers and crews

def categorizer(value):
    if 'PASSENGER' in value.upper():
        return 'Passenger'
    else:
        return 'Crew'
data_trim['Crew/Passenger'] = data_trim['Class/Dept'].map(str).apply(categorizer)
data_trim.head()

	Name	Age	Class/Dept	Boat [Body]	Crew/Passenger
0	ABBING, Mr Anthony	42.0	3rd Class Passenger	nan	Passenger
1	ABBOTT, Mrs Rhoda Mary 'Rosa'	39.0	3rd Class Passenger	A	Passenger
2	ABBOTT, Mr Rossmore Edward	16.0	3rd Class Passenger	[190]	Passenger
3	ABBOTT, Mr Eugene Joseph	13.0	3rd Class Passenger	nan	Passenger
4	ABBOTT, Mr Ernest Owen	21.0	Victualling Crew	nan	Crew

Check passenger ticket class

def get_passenger_class(value):
    if 'PASSENGER' in value.upper():
        return value.split(' ')[0]
    else:
        return 'Crew'
data_trim['Class'] = data_trim['Class/Dept'].map(str).apply(get_passenger_class)
data_trim.head()

	Name	Age	Class/Dept	Boat [Body]	Crew/Passenger	Class
0	ABBING, Mr Anthony	42.0	3rd Class Passenger	nan	Passenger	3rd
1	ABBOTT, Mrs Rhoda Mary 'Rosa'	39.0	3rd Class Passenger	A	Passenger	3rd
2	ABBOTT, Mr Rossmore Edward	16.0	3rd Class Passenger	[190]	Passenger	3rd
3	ABBOTT, Mr Eugene Joseph	13.0	3rd Class Passenger	nan	Passenger	3rd
4	ABBOTT, Mr Ernest Owen	21.0	Victualling Crew	nan	Crew	Crew

Check Adult/Child

def check_adult(age):
    if age > 18:
        return 'Adult'
    else:
        return 'Child'
data_trim['Adult/Child'] = data_trim['Age'].apply(check_adult)
data_trim.head()

	Name	Age	Class/Dept	Boat [Body]	Crew/Passenger	Class	Adult/Child
0	ABBING, Mr Anthony	42.0	3rd Class Passenger	nan	Passenger	3rd	Adult
1	ABBOTT, Mrs Rhoda Mary 'Rosa'	39.0	3rd Class Passenger	A	Passenger	3rd	Adult
2	ABBOTT, Mr Rossmore Edward	16.0	3rd Class Passenger	[190]	Passenger	3rd	Child
3	ABBOTT, Mr Eugene Joseph	13.0	3rd Class Passenger	nan	Passenger	3rd	Child
4	ABBOTT, Mr Ernest Owen	21.0	Victualling Crew	nan	Crew	Crew	Adult

Check Gender

def check_gender(name):
    firstname = name[name.index(',')+2:]
    salutation = firstname.split(' ')[0]
    if salutation.upper() in ['MR', 'MASTER']:
        return 'Male'
    else:
        return 'Female'

data_trim['Gender'] = data_trim['Name'].map(str).apply(check_gender)
data_trim.head()

	Name	Age	Class/Dept	Boat [Body]	Crew/Passenger	Class	Adult/Child	Gender
0	ABBING, Mr Anthony	42.0	3rd Class Passenger	nan	Passenger	3rd	Adult	Male
1	ABBOTT, Mrs Rhoda Mary 'Rosa'	39.0	3rd Class Passenger	A	Passenger	3rd	Adult	Female
2	ABBOTT, Mr Rossmore Edward	16.0	3rd Class Passenger	[190]	Passenger	3rd	Child	Male
3	ABBOTT, Mr Eugene Joseph	13.0	3rd Class Passenger	nan	Passenger	3rd	Child	Male
4	ABBOTT, Mr Ernest Owen	21.0	Victualling Crew	nan	Crew	Crew	Adult	Male

def check_survival(value):
    if value.strip()=='nan' or '[' in value:
        return 0
    else:
        return 1
data_trim['Survival'] = data_trim['Boat [Body]'].map(str).apply(check_survival)
data_trim.head()

	Name	Age	Class/Dept	Boat [Body]	Crew/Passenger	Class	Adult/Child	Gender	Survival
0	ABBING, Mr Anthony	42.0	3rd Class Passenger	nan	Passenger	3rd	Adult	Male	0
1	ABBOTT, Mrs Rhoda Mary 'Rosa'	39.0	3rd Class Passenger	A	Passenger	3rd	Adult	Female	1
2	ABBOTT, Mr Rossmore Edward	16.0	3rd Class Passenger	[190]	Passenger	3rd	Child	Male	0
3	ABBOTT, Mr Eugene Joseph	13.0	3rd Class Passenger	nan	Passenger	3rd	Child	Male	0
4	ABBOTT, Mr Ernest Owen	21.0	Victualling Crew	nan	Crew	Crew	Adult	Male	0

Check the importance of each feature

def entropy_calculate(prob_list):

    entropy = 0
    for item in prob_list:
        entropy -= item * np.log2(item)
    return entropy

def information_gain(feature, data, initial_entropy):
    print('Information gain analysis for {}'.format(feature))
    probability_l1 = data.groupby([feature])['Survival'].count()/len(data)
    entropy_feature=0
    for item, probabality in probability_l1.items():
        print('\tProbability of {}:'.format(item), probabality)
        probability_l2 = data[data[feature]==item].groupby(['Survival'])['Survival'].count()/len(data[data[feature]==item])

        entropy_feature += entropy_calculate(probability_l2) * probabality
    print('\n\tEntropy of feature: %.3f'%(entropy_feature))
    print('\tInformation gain: %.3f'%(initial_entropy - entropy_feature))

Information gain analysis

probability_initial = data_trim.groupby(['Survival'])['Survival'].count()/len(data_trim)
initial_entropy = entropy_calculate(probability_initial)
print('Initial entropy: %.3f'%(initial_entropy))

Initial entropy: 0.815

information_gain(feature='Crew/Passenger', data=data_trim, initial_entropy=initial_entropy)

Information gain analysis for Crew/Passenger
        Probability of Crew: 0.4543987086359968
        Probability of Passenger: 0.5456012913640033

        Entropy of feature: 0.772
        Information gain: 0.043

information_gain(feature='Class', data=data_trim, initial_entropy=initial_entropy)

Information gain analysis for Class
        Probability of 1st: 0.14124293785310735
        Probability of 2nd: 0.11824051654560129
        Probability of 3rd: 0.2861178369652946
        Probability of Crew: 0.4543987086359968

        Entropy of feature: 0.738
        Information gain: 0.077

information_gain(feature='Adult/Child', data=data_trim, initial_entropy=initial_entropy)

Information gain analysis for Adult/Child
        Probability of Adult: 0.880548829701372
        Probability of Child: 0.11945117029862792

        Entropy of feature: 0.813
        Information gain: 0.003

information_gain(feature='Gender', data=data_trim, initial_entropy=initial_entropy)

Information gain analysis for Gender
        Probability of Female: 0.23284907183212267
        Probability of Male: 0.7671509281678773

        Entropy of feature: 0.702
        Information gain: 0.113

Pick features and lable to construct the decision tree

training_data = data_trim[['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender','Survival']]
training_data.head()

	Age	Crew/Passenger	Class	Adult/Child	Gender	Survival
0	42.0	Passenger	3rd	Adult	Male	0
1	39.0	Passenger	3rd	Adult	Female	1
2	16.0	Passenger	3rd	Child	Male	0
3	13.0	Passenger	3rd	Child	Male	0
4	21.0	Crew	Crew	Adult	Male	0

Process categorical variables to numerical

category_map ={}
for column in ['Crew/Passenger','Class','Adult/Child','Gender']:
    category_map[column] = dict( enumerate(training_data[column].astype('category').cat.categories) )
    training_data[column] = training_data[column].astype('category').cat.codes

training_data.head()

	Age	Crew/Passenger	Class	Adult/Child	Gender	Survival
0	42.0	1	2	0	1	0
1	39.0	1	2	0	0	1
2	16.0	1	2	1	1	0
3	13.0	1	2	1	1	0
4	21.0	0	3	0	1	0

training_data.dropna(inplace=True)
training_data.reset_index(drop=True, inplace=True)
print('Total number of valid records: {}'.format(len(training_data)))

Total number of valid records: 2449

Split to train and test data

from sklearn.model_selection import train_test_split

train, test = train_test_split(training_data, test_size=0.2)
train.reset_index(drop=True, inplace=True)
test.reset_index(drop=True, inplace=True)

print('Total number of records used for training: {}\nTotal number of records used for testin: {}'.format(len(train),len(test)))

Total number of records used for training: 1959
Total number of records used for testin: 490

Build a decision tree

from sklearn.tree import DecisionTreeClassifier

X = train[['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender']]
y = train[['Survival']]

clf = DecisionTreeClassifier(max_leaf_nodes=20, criterion='entropy')

clf = clf.fit(X, y)

clf

DecisionTreeClassifier(class_weight=None, criterion='entropy', max_depth=None,
            max_features=None, max_leaf_nodes=20,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, presort=False, random_state=None,
            splitter='best')

• class_weight: A dictionary to provide user defined weights for each feature

• criterion: The criterion is the method used to decide with label and what decision needs to be made. gini impurity and information gain/entropy are the two main methods

• max_depth: It determines the maximum depth/layer from the root of the tree to the finest leaf

• max_features: if you want you can ask the algorithm to use a limited number of features based on their importance. This could be a dimension reduction approach that can simplify the tree

• max_leaf_nodes: The max number of end nodes that is another stopping criteria for the decision tree

• min_impurity_split: The minimum amount of impurity split percentage that result in generating another branch. In case of information gain, this will be measured by the amount/percentage of reduction in entropy.

• min_samples_leaf: Minimum number of samples that should exist in a subset created by a decision. If less than this number, the branch gets pruned and the previous level of the tree will be kept

• min_samples_split: Minimum number of samples in a tree level to consider further splitting and decision making

• min_weight_fraction_leaf: similar to min_samples_leaf but expressed as a fraction of whole data

• random_state, presort and splitter are performance related settings and do not affect the algorithm

clf.feature_importances_

array([0.20502926, 0.        , 0.28082862, 0.        , 0.51414211])

As can be seen above, the importance analysis confirms the result of information gain analysis that Gender is the most important feature.

Tree visualization

from sklearn import tree

with open ('Outputs/Titanic.dot', 'w') as f:
    f = tree.export_graphviz(clf, feature_names=['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender'], out_file=f)

# conda install -c conda-forge python-graphviz
from graphviz import Source

s = Source.from_file('Outputs/Titanic.dot')
s.render() # saves a pdf file
s

Evaluate the tree

Using train and test data sets

from sklearn.metrics import accuracy_score

predictions = clf.predict(test.drop(['Survival'], axis=1))

accuracy_score(test['Survival'],predictions)

0.8224489795918367

It is possible to tune the decision tree parameters based on the accuracy measure. For example the max_leaf_nodes can be tuned to find the maximum accuracy.

K-fold cross validation

from sklearn.model_selection import cross_val_predict, cross_val_score

X = training_data[['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender']]
y = training_data[['Survival']]

cross_val_score(clf, X, y, cv=5)

array([0.82244898, 0.81428571, 0.79795918, 0.78367347, 0.81799591])

Ensemble learning to avoid over fitting

The ensemble learning relies on using multiple instances of a machine learning algorithm (i.e. decision tree) that are trained with different subsets of the available training data. Also, the algorithm parameters and number of used features may be different for each instance.

Each instance might be over/under fitted based on used data. However, the ensemble response is determined based on a majority rule decision.

In other words, an ensemble may be defined as a collection of models (even different types) that solve the same problem. However, the final answer is achieved by a combining the response of all the models.

Random Forest

A collection of decision trees are built and trained independently and the combination provides the final response.

• Each tree in ensemble is built from a different subset of the training set (using Bagging (bootstrap aggregating) technique)

• Each tree in ensemble is built using a different subset of features (using random subspace technique)

from sklearn.ensemble import RandomForestClassifier

clf = RandomForestClassifier()
clf

RandomForestClassifier(bootstrap=True, class_weight=None, criterion='gini',
            max_depth=None, max_features='auto', max_leaf_nodes=None,
            min_impurity_decrease=0.0, min_impurity_split=None,
            min_samples_leaf=1, min_samples_split=2,
            min_weight_fraction_leaf=0.0, n_estimators=10, n_jobs=1,
            oob_score=False, random_state=None, verbose=0,
            warm_start=False)

Most of the parameters are related to settings of a decision tree. Settings related to the ensemble learning (i.e. the random forest) are explained below.

• bootstrap: Using the bootstrap technique to randomly select different subsets of data for each tree

• n_estimators: number of trees

clf.fit(X = train[['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender']], y=train[['Survival']])
predictions = clf.predict(test.drop(['Survival'], axis=1))
print('Accuracy : %.2f'%(accuracy_score(test['Survival'], predictions)))

Accuracy : 0.81

for feature, importance in zip(['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender'],clf.feature_importances_):
    print('Importance for {} : {:.3f}'.format(feature,importance))

Importance for Age : 0.450
Importance for Crew/Passenger : 0.052
Importance for Class : 0.185
Importance for Adult/Child : 0.009
Importance for Gender : 0.304

# Using the train/test data
def checkAccuracy(n_estimators=10):
    clf = RandomForestClassifier(n_estimators=n_estimators, criterion='entropy')
    X = train[['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender']]
    y=train[['Survival']]
    return np.mean(cross_val_score(clf, X, y, cv=5).mean())

result ={'Number of trees':[], 'AccuracyScore': []}
for n_tree in np.arange(1, 500, 10):
    result['Number of trees'].append(n_tree)
    result['AccuracyScore'].append(checkAccuracy(n_estimators=n_tree))

result_df = pd.DataFrame.from_dict(result)
result_df.head()

	Number of trees	AccuracyScore
0	1	0.773856
1	11	0.789191
2	21	0.792767
3	31	0.789701
4	41	0.788175

result_df.plot(x='Number of trees', y='AccuracyScore', figsize=(10,5), grid=True, lw=3, color='orange')

<matplotlib.axes._subplots.AxesSubplot at 0x14197cd6908>

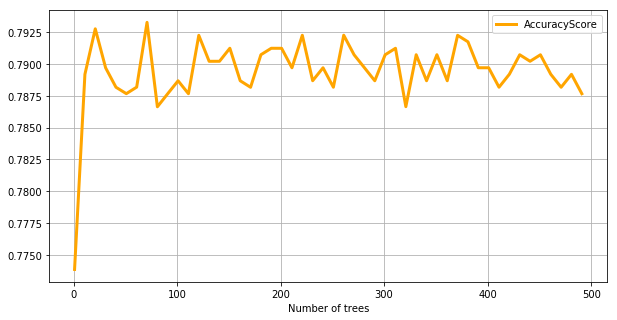
As can be seen above, adding more trees provides a better classification accuracy on average. However, this doe not mean that adding more tress will necessarily always result in a better accuracy depending on the cross validation population.

Gradient Boosted Trees

Each tree is built based on learnings of the previous tree

Each tree is trained using a different subset of data. However, the Boosting + Gradient Descent techniques are used to pool the subsets. After the bootstrap for one tree, Gradient Descent adjusts the probability of a data point being in the next training set and this continues sequentially. In this context, while the first bootstrap is based on uniform sampling the next one is modified based on what was learned from the previous three classification results. Data points that are classified correctly get lower weight for the next bootstrap. In this way, the likelihood of picking data that are not classified with previous tree increases. Finally, each tree is given a different weight for the final weighting for the majority rule decision.

I random forest, there is a “democracy” that all trees have the same voting weights. However, in the gradient boosted approach, trees that have a better performance/accuracy get a higher weight. Gradient descent is one of the technique that can be used to quantify the probability of choosing a data point in the train subset based on the result of the previous tree.

For window installation:

conda install -c anaconda py-xgboost

A rule of thumb is to use a lower number of tree when dealing with a small training data set.

from xgboost.sklearn import XGBClassifier

clf = XGBClassifier()
clf

XGBClassifier(base_score=0.5, booster='gbtree', colsample_bylevel=1,
       colsample_bytree=1, gamma=0, learning_rate=0.1, max_delta_step=0,
       max_depth=3, min_child_weight=1, missing=None, n_estimators=100,
       n_jobs=1, nthread=None, objective='binary:logistic', random_state=0,
       reg_alpha=0, reg_lambda=1, scale_pos_weight=1, seed=None,
       silent=True, subsample=1)

• colsample_bylevel: Fraction of features used by each tree

• learning_rate: Controls the probability manipulation of data records based on the previous tree. Increasing this factor results in an increased focus on data records that were miss-classified.

• subsample: Fraction of the provided training data set used for each tree. Lowering this number results in a more distinct difference between training data sets used for each tree

• gamma: Minimum reduction in error to split the tree further

• n_estimators: Number of trees

clf.fit(X = train[['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender']], y=train[['Survival']])
predictions = clf.predict(test.drop(['Survival'], axis=1))
print('Accuracy : %.2f'%(accuracy_score(test['Survival'], predictions)))

Accuracy : 0.82

for feature, importance in zip(['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender'],clf.feature_importances_):
    print('Importance for {} : {:.3f}'.format(feature,importance))

Importance for Age : 0.629
Importance for Crew/Passenger : 0.057
Importance for Class : 0.221
Importance for Adult/Child : 0.000
Importance for Gender : 0.093

Hyper Parameter Tuning

Considering the different parameters that affect the performance of a decision tree and also parameters that control the ensemble learning, there are many combinations that should be checked to find the best accuracy for the train/test data set. Hyper parameter tuning uses optimization technique to find an optimal combination.

# conda install -c jaikumarm hyperopt
from hyperopt import fmin, tpe, hp, STATUS_OK, Trials

# provide the optimization range/population
control = {
    'n_estimators': hp.quniform('n_estimators',100,1000,1)
    ,'learning_rate': hp.quniform('learning_rate', 0.1,0.4,0.1)
    ,'max_depth': hp.quniform('max_depth',1,15,1)
    ,'min_child_weight': hp.quniform('min_child_weight',1,6,1)
    ,'subsample': hp.quniform('subsample',0.5,1,0.05)
    ,'gamma': hp.quniform('gamma', 0.5,1,0.05)
    ,'colsample_bytree': hp.quniform('colsample_bytree',0.5,1,0.05)
    ,'nthread':5
    ,'silent':1
}

def scorevalue(clf):
    X = train[['Age', 'Crew/Passenger', 'Class', 'Adult/Child', 'Gender']]
    y=train[['Survival']]
    return np.mean(cross_val_score(clf, X, y, cv=5).mean())

# Define a score that gets minimized and provides what you need
def score(params):
    params['n_estimators'] = int(params['n_estimators'])
    params['max_depth'] = int(params['max_depth'])
    clf = XGBClassifier(**params)
    return {'loss':1-scorevalue(clf), 'status':STATUS_OK}

trails=Trials()

best_param_set = fmin(score,control,algo=tpe.suggest,trials=trails,max_evals=250)

print('Optimized parameters: ')
for key, value in best_param_set.items():
    print('{} = {}'.format(key,value))

Optimized parameters:
colsample_bytree = 1.0
gamma = 1.0
learning_rate = 0.2
max_depth = 10.0
min_child_weight = 5.0
n_estimators = 583.0
subsample = 1.0

print('Optimized Accuracy: {:.3f}'.format(1-score(best_param_set)['loss']))

Optimized Accuracy: 0.816